ת.ז- קרל פרידריך גאוס
שם: קרל פרידריך גאוס.
שנות פעילותיו: 30 באפריל 1777- 23 בפבואר 1855.
היכן נולד: בבראונשווייג.
מידע כללי: גאוס נולד בבראונשווייג שבסקסוניה תחתית כבן יחיד למשפחת פועלים ענייה. גאוס עצמו סיפר כי עמד על סוד הפעולות האריתמטיות עוד בטרם ידע לדבר. קיימים סיפורים רבים על גאונותו כילד, אחד מהם, המובא בספרו של אריק טמפל בל, הוא כי עוד בטרם מלאו לו 3 שנים, נתגלה להוריו כשרונו המתמטי הייחודי: אביו עסק בהכנת גיליון השכר השבועי של הפועלים שבהשגחתו וביצע במשך דקות ארוכות את החישובים המסובכים. כאשר סיים את החישוב, אמר לו בנו שנפלה טעות בחישוב, ונקב בתוצאה שחישב בראשו. עוד סיפור מפורסם מבית הספר היסודי מספר כי מורהו של גאוס ביקש להעסיק את תלמידי הכיתה בתרגיל שלפתרונו הייתה דרושה שעה ארוכה. התרגיל היה לחבר את המספרים מ-1 עד 100, והנה לא עברו כמה שניות וגאוס, באותה עת בן 7 בלבד, הניח את לוח-היד וקרא "!Lieget se" ("הנה זה מונח", בניב המקומי) ונתן את הסכום: 5,050. בדיעבד התברר כי הוא גילה את הטור החשבוני בלי להיות מודע לכך: הוא הבחין שסכום האיבר הראשון והאחרון זהה לסכום האיבר השני והלפני האחרון וכן הלאה (1 + 100, 2 + 99, ..., 50 + 51). מה שצריך היה לעשות הוא להכפיל 101 כפול מספר הזוגות (שהוא מחצית מספר האיברים-50), וכך מתקבל הפתרון. התחלת המחקר המתמתי: גאוס קיבל מלגה מהדוכס ובשנים 1792 עד 1795 למד ב-Collegium Carolinum.
משם המשיך ללימודים גבוהים באוניברסיטת גטינגן שם למד עד 1798.
בעודו באוניברסיטה, גאוס גילה מחדש באופן בלתי תלוי מספר משפטים חשובים. הפריצה שלו התרחשה ב-1796, כאשר הראה באמצעות הרעיון של הרחבת שדות שכל מצולע משוכלל שמספר צלעותיו הוא מספר פרמה ניתן לבנייה בסרגל ומחוגה. תגלית זו הייתה ההתקדמות המשמעותית הראשונה בנושא בניות בסרגל ומחוגה מזה למעלה מ-2000 שנה.
תחומי חקר: האלגברה, תורת המספרים, גאודזיה, תורת הכבידה, תורת החשמל, אסטרונומיה, אופטיקה ועוד.
תחילץ פרסומו: תחילת פרסומו התרחשה ב-1796, כאשר הראה באמצעות הרעיון של הרחבת שדות שכל מצולע משוכלל שמספר צלעותיו הוא מספר פרמה (ועקב כך כל מכפלה של מספר פרמה בחזקה של 2) ניתן לבנייה בסרגל ומחוגה. תגלית זו הייתה ההתקדמות המשמעותית הראשונה בנושא בניות בסרגל ומחוגה מזה למעלה מ-2000 שנה.
המיוחד בממצאיו מחריו ותגליותיו:
קרל פרידריך גאוס הוא שבעודו באוניברסיטה, גאוס גילה מחדש באופן בלתי תלוי מספר משפטים חשובים. הפריצה שלו התרחשה ב-1796, כאשר הראה באמצעות הרעיון של הרחבת שדות שכל מצולע משוכלל שמספר צלעותיו הוא מספר פרמה (ועקב כך כל מכפלה של מספר פרמה בחזקה של 2) ניתן לבנייה בסרגל ומחוגה. תגלית זו הייתה ההתקדמות המשמעותית הראשונה בנושא בניות בסרגל ומחוגה מזה למעלה מ-2000 שנה - בעיות בנייה העסיקו מתמטיקאים עוד מאז ימי המתמטיקאים היוונים העתיקים, והייתה לה חשיבות רבה בהתפתחות האלגברה, הן בזכות הכנסת המישור המרוכב לשימוש, והן בזכות פתיחת שערים לתאוריות מתמטיות עמוקות כמו תורת גלואה.

 , אז
, אז 
 ,
, ו-
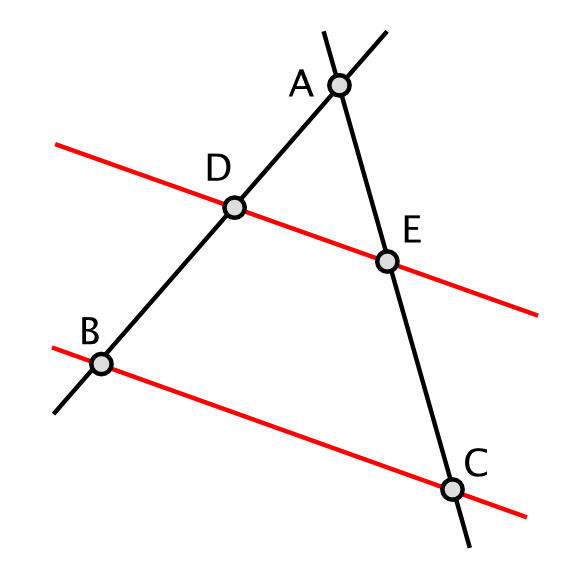
ו- מונחות על מעגל והקו
מונחות על מעגל והקו  עובר דרך מרכז המעגל, אז הזווית
עובר דרך מרכז המעגל, אז הזווית  שווה לתשעים מעלות:
שווה לתשעים מעלות:
 בין מרכז המעגל החוסם ומרכז המעגל החסום של משולש מקיים:
בין מרכז המעגל החוסם ומרכז המעגל החסום של משולש מקיים:  , כאשר
, כאשר  הוא רדיוס המעגל החוסם ו-
הוא רדיוס המעגל החוסם ו- הוא רדיוס המעגל החסום.
הוא רדיוס המעגל החסום. .
. וכן
וכן (זווית חיצונית שווה לסכום שתי הזוויות האחרות במשולש),
(זווית חיצונית שווה לסכום שתי הזוויות האחרות במשולש), ,
, הוא כוח הציפה הפועל על גוף
הוא כוח הציפה הפועל על גוף מציין את צפיפות החומר של התווך
מציין את צפיפות החומר של התווך  מציין את נפח הגוף שנמצא בתוך התווך, ועליו פועל כוח הציפה
מציין את נפח הגוף שנמצא בתוך התווך, ועליו פועל כוח הציפה
 .
.

 או
או  .
. .
. הגבוהה ביותר שעבורה המקדם
הגבוהה ביותר שעבורה המקדם  שונה מאפס, היא המעלה של הפולינום. המקדם
שונה מאפס, היא המעלה של הפולינום. המקדם  נקרא המקדם החופשי ו-
נקרא המקדם החופשי ו-  נקרא המקדם המוביל של הפולינום. אם המקדם המוביל שווה ל- 1, אז הפולינום נקרא פולינום מתוקן. לדוגמה,
נקרא המקדם המוביל של הפולינום. אם המקדם המוביל שווה ל- 1, אז הפולינום נקרא פולינום מתוקן. לדוגמה,  הוא פולינום ממעלה שנייה, שהמקדם המוביל שלו הוא 3.
הוא פולינום ממעלה שנייה, שהמקדם המוביל שלו הוא 3.